Rishabh-Singh

Time Series Data Analysis using Kernel Uncertainty Framework

Decomposition of time series signal using QIPF uncertainty framework.
Abstract and Goal we propose to utilize the QIPF framework which provides a completely data-adaptive and multi-moment uncertainty representation of a signal and is consequently able to quantify the local dynamics at each point in the sample space in an unsupervised manner with high sensitivity and specificity with repect ot the overall signal PDF. Through the use of the QIPF, we utilize concepts of quantum physics (which provides a principled quantification of particle-particle dynamics in a physical system) to interpret data. Consequently we introduce a new energy based information theoretic formulation to accomplish pattern recognition tasks associated with time series data that quantifies sample-by-sample dynamics of the signal (important in online time series analysis, which is not achievable by conventional methods). We specifically explore applications like anomaly detection and clustering.


Approach:

Our approach consists of three main steps:

\(\mathbf{1}\). Estimation of PDF at a sample at time \(t\) using information potential field (empirical estimate of kernel mean embedding):

\(p(x^t|x^0, x^1 ... x^{t-1}) \approx \psi_{\mathbf{x}}(x^t) = \frac{1}{n}\sum_{k=1}^{t-1}G_\sigma(x_k, x^t)\).

\(\mathbf{2}\). A Schrödinger’s equation formulation over data PDF by assuming the IFP, \(\psi_{\mathbf{x}}(x^t)\), to be a wave-function. This transforms the static PDF measure (the IPF) into a dynamic embedding that measures the local changes in the PDF at \(x^t\):

\(H_(x^t) = E_\mathbf{w}(x^t) + (\sigma^2/2)\frac{\nabla_y^2\psi_\mathbf{w}(x^t)}{\psi_\mathbf{w}(x^t)}\)

\(\mathbf{3}\). Moment decomposition of \(H\) to extract various uncertainty modes at \(x^t\) which serve as dynamical features of the time-series at time t:

\(H^k(x^t) = E_\mathbf{w}^k(x^t) + (\sigma^2/2)\frac{\nabla_y^2\psi_\mathbf{w}^k(x^t)}{\psi_\mathbf{w}^k(x^t)}\).

These stochastic features \(H^0(x^t), H^1(x^t), H^2(x^t) ...\) are then utilized for applications like clustering or detection of change points in the time-series.

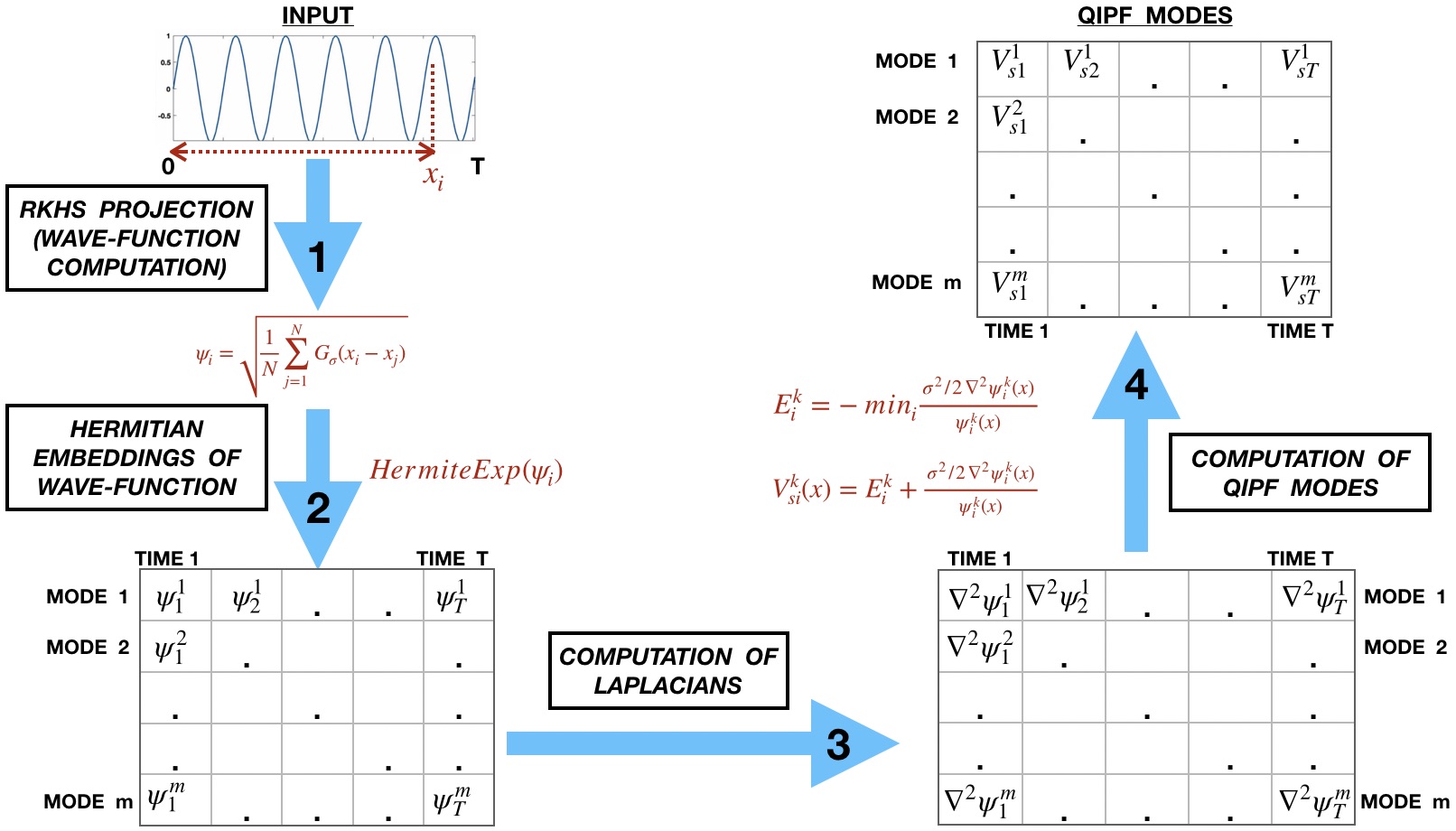
Detailed depiction of approach: QIPF uncertainty decomposition of a time series.


Algorithm:

A pseudo-code for QIPF implementation is as follows:


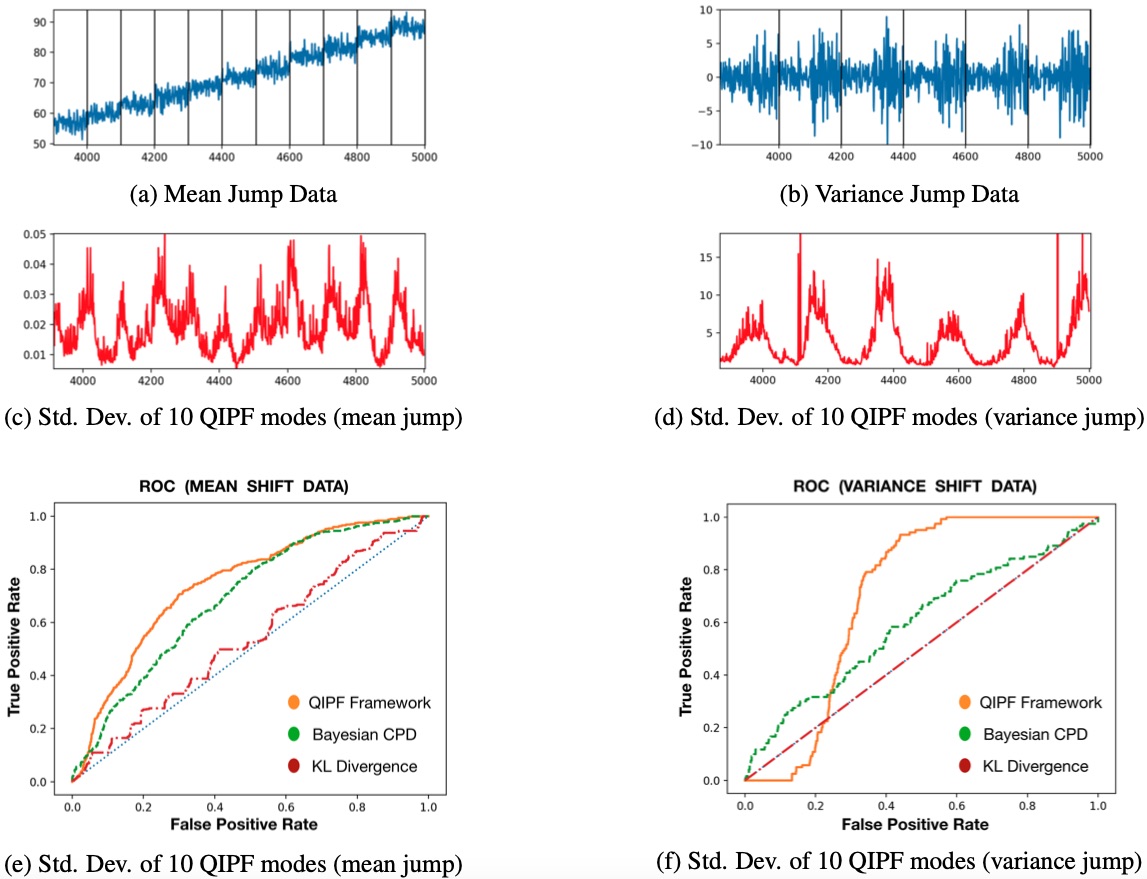
Results:

Analysis of mode locations of the sine wave in the space of data using different kernel widths. Solid colored lines represent the different QIPF modes. Dashed line represents the IPF.



Change point detection in time series: Last 1000 samples of drift datasets (top row), their corresponding QIPF mode standard deviations measured at each point (middle row) and corresponding the ROC curves (bottom row) for different methods measured in the range of 2000-3000 samples for both datasets. Black vertical lines (in the top row) mark the actual change points.


Singh, R. and Principe, J., 2020, August. Time Series Analysis using a Kernel based Multi-Modal Uncertainty Decomposition Framework. In Conference on Uncertainty in Artificial Intelligence (pp. 1368-1377). PMLR. (Paper Link)

Abstract
This paper proposes a kernel based information theoretic framework with quantum physical underpinnings for data characterization that is relevant to online time series applications such as unsupervised change point detection and whole sequence clustering. In this framework, we utilize the Gaussian kernel mean embedding metric for universal characterization of data PDF. We then utilize concepts of quantum physics to impart a local dynamical structure to characterized data PDF, resulting in a new energy based formulation. This facilitates a multi-modal physics based uncertainty representation of the signal PDF at each sample using Hermite polynomial projections. We demonstrate in this paper using synthesized datasets that such uncertainty features provide a better ability for online detection of statistical change points in time series data when compared to existing non-parametric and unsupervised methods. We also demonstrate a better ability of the framework in clustering time series sequences when compared to discrete wavelet transform features on a subset of VidTIMIT speaker recognition corpus.