RKHS based Physical Interpretation of Model Uncertainty: The QIPF
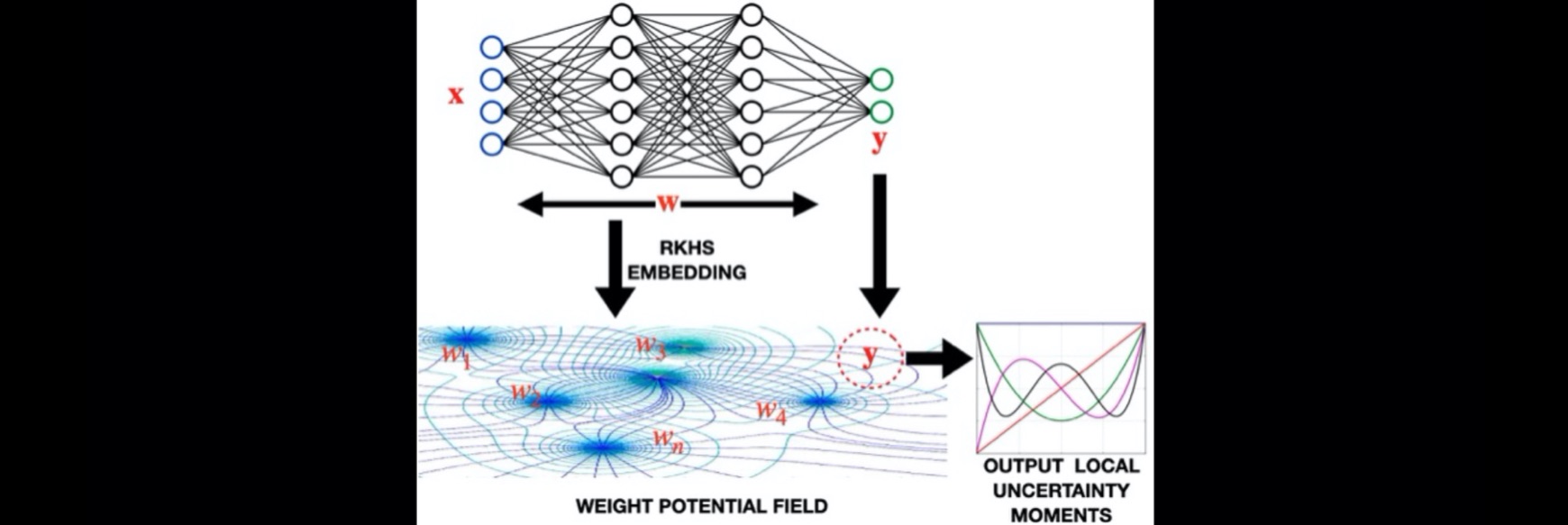Approach: Moments extracted from the local interaction of the model output with the RKHS potential field of the weights quantify the output uncertainty.
We combine the expressive power of the Gaussian reproducing kernel Hilbert space (RKHS) and the high local resolution provided by quantum physics to create a moment decomposition framework for quantifying the predictive uncertainty of neural network models. The framework, called the quantum information potential field (QIPF), replaces the convention Bayesian notion of weight PDF with a physics based potential field representation of the model weights in a Gaussian RKHS. The QIPF moments quantify predictive uncertainty of a model by measuring the local interaction of a model prediction with its weight potential field. We show that the QIPF uncertainty measures are significantly more precise and better calibrated than Bayesian methods, especially in presence of distributional shifts in test-set, while being much cheaper to compute.
Click here to read more!
Transfer Learning Uncertainty Quantification using QIPF (ongoing)
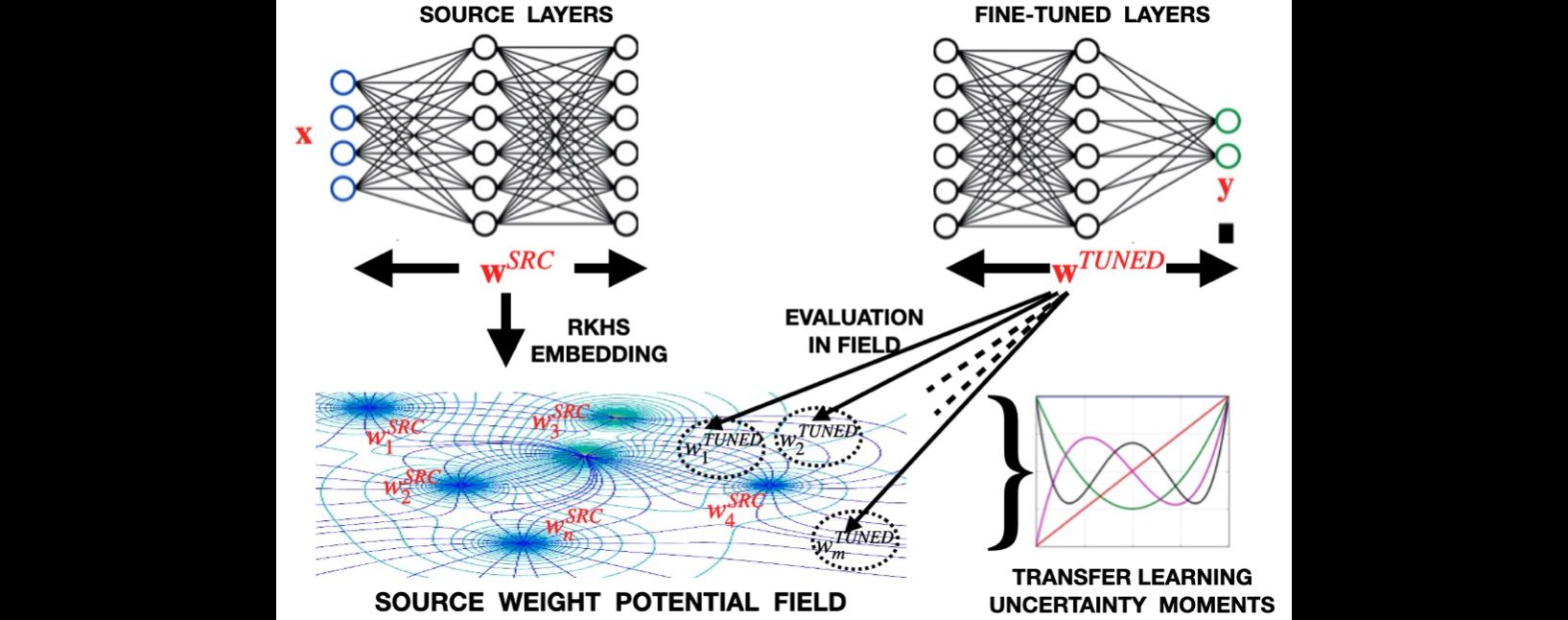Approach: Moments extracted from the local interaction of the fine-tuned layer weights with the RKHS potential field created by source layer weights quantify the overall uncertainty in modeling target dataset.
We extend the application of QIPF for quantifying transfer learning uncertainty. Here, we utilize the QIPF to quantify the overall predictive uncertainty of a model originally trained on a source dataset and then fine-tuned on a target dataset by evaluating the weights of the fine-tuned layers on the RKHS potential field created by source layer weights. This gives the discrepancy (with respect ot the model) between source and target datasets.
Click here to read more!
Time Series Data Analysis using Kernel Uncertainty Framework
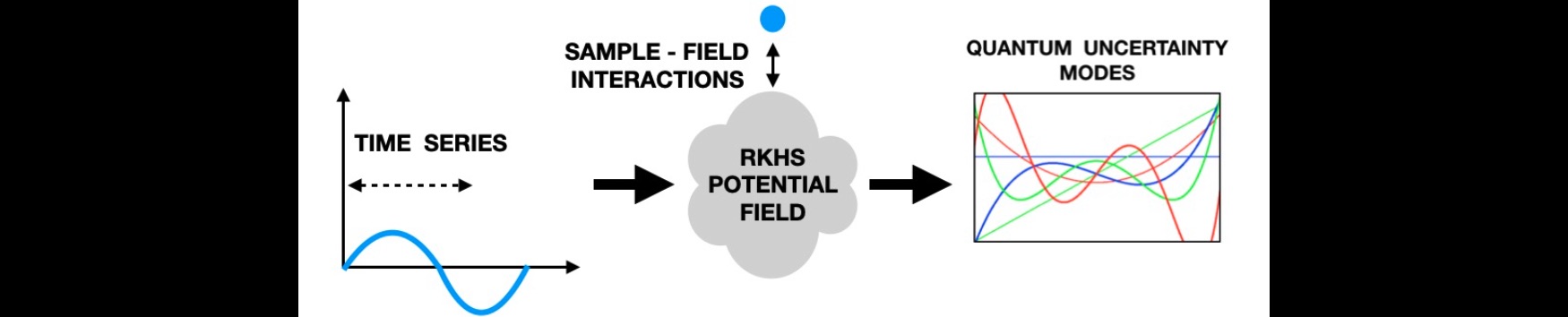Decomposition of time series signal using QIPF uncertainty framework.
In this work, we utilize the QIPF, an RKHS based uncertainty decomposition framework, to obtain a physical viewpoint of time series signal dynamics. More concretely, we leverage the QIPF as a dynamic potential field (embedding space) that automatically and sensitively adapts its local structure according to data, for the analysis of time series signals. We consequently arrive at an energy-based formulation of the time series signal that is now represented in terms of multiple moments of uncertainty at each data sample. Preliminary experiments show that QIPF features of time series data can be very useful for applications like anomaly detection and clustering.
Click here to read more!
Hierarchical Linear Dynamical System
The Hierarchical Linear Dynamical System (HLDS) is a modified Kalman filter based topology of linear dynamical system (LDS) where we impose prior structural constraints of systematically varying proportions on the states. This induces unsupervised clustering of signal dynamics (being modeled by the LDS) at its most constrained states, thereby naturally improving its ability to model complex data sequences. I made the following contributions in the development and application of this algorithm.
1. Demonstrated better ability of the HLDS in modeling layered dynamic textures (a complex multi-dimensional and multi-dynamical data sequence where one or more texture videos are imposed over another) when compared with LDS. Visit paper for details
2. Introduced Correntropy cost function for the HLDS to further improve its localization ability of the signal in its constrained states. This made it possible for the HLDS (despite being a linear algorithm) to cluster different speech phonemes. Visit paper for details
3. Deployed HLDS for video game action sequence segmentation as part of a preliminary downstream task in a DARPA funded project: “An Active Architecture for Self Learning”. Link to Project Abstract